前回は、予測と実際の結果がどれほど一致するか検証してみた。
具体的には、k-folds cross validationやconfusion matrix(混合行列)について、実際の手書きの数字画像データを利用して検証してみた。
理由は、検証はとても大事だからだ。
極端な例だが、10個のデータがあって9個のデータが陽性だとしよう。
すべてのデータは陽性だと予測しても、正解率は90%になる。
しかし、陰性に対する予測が全くできていないので、正解率をチェックするだけでは不十分だ。
そこで、適合率と再現率を紹介したが、今回は落とし所をどうやって決めるのか見ていこう。
Precision/Recall Curve (適合率/再現率曲線)
起こり得る適合率と再現率の組み合わせを表す曲線が適合率/再現率曲線だ。
言葉だけではイメージしずらいので、実際に見てみよう。
def plot_precision_vs_recall(precisions, recalls):
plt.plot(recalls, precisions, "b-", linewidth=2)
plt.xlabel("Recall", fontsize=10)
plt.ylabel("Precision", fontsize=10)
plt.axis([0, 1, 0, 1])
plt.figure(figsize=(7, 5))
plot_precision_vs_recall(precisions, recalls)
plt.show()
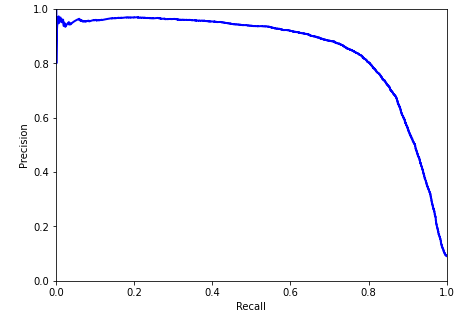
PrecisionはRecallが80%ぐらいのところから急激に下がっていることがわかる。どの割合がただしいというのはないので、あらかじめ最低限保証したい値を決めておくのがいいだろう。
Threshold (閾値)
例えば、Precision(適合率)が90%がゴールとしよう。Recallの値は、なんだろうか?
適合率/再現率曲線からもわかるが、つぎのようにargmax()を使って最大値をとるインデックスのうち、もっとも小さいインデックスを求めることができる。

つまり、Recall(再現率)は、66%ぐらいになる。
ちなみに、適合率が95%だと、再現率は、43%になる。
まとめ
今回は、起こり得る適合率と再現率の組み合わせを表す曲線を紹介した。どのパターンが最適かは、じつは目的によってことなる。例えば、癌の陽性を発見するタスクでは、陽性患者を陰性と判断してはマズいので、陰性の患者を陽性と診断して、再検査したほうがマシなのだ。



コメント