前回は、info()、describe()メソッドを使って、データの中身について学んだ。また、ヒストグラムをshow()することによって、Jupyter Notebookでグラフを描いてみた。
今回は、データから地図を表示してみよう。といっても、普通の地図ではなく、経度と緯度の情報から作成する地図だ。
また、データの相関係数を数値化して、どれほど相関があるのか調べてみよう。
plot()メソッド
pandasのplot()メソッドを使って、簡単にグラフを作成できる。
前回ロードしたデータには、経度と緯度の情報があるので、x=”longitude” y=”latitude”として散布図(scatter plot)を描いてみよう。
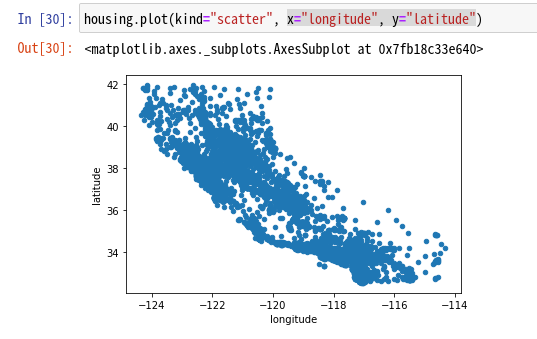
なんとなくカリフォルニアの形を認識できるだろう。ただし、密度については指定していないので、色の濃さが同じだ。
そこで、alphaと呼ばれる透過率を指定することによって、データの密度の濃い部分を強調することができる。
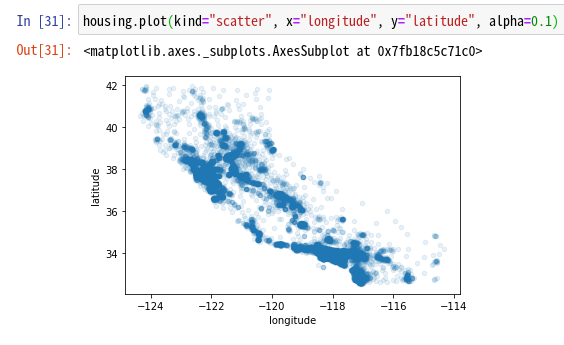
San FranciscoのベイエリアとLos Angeles周辺が混みあっていることがわかる。
この散布図にpopulationとmedian_house_valueを追加してみよう。関連するプロパティーが多数でてくるので、以下を参考にしてほしい。
| alpha | 透過率。0(透明) ~ 1(不透明) |
| c | 色 |
| cmap | カラーマップ。rainbowやjetなどがある。 |
| s | サイズ |
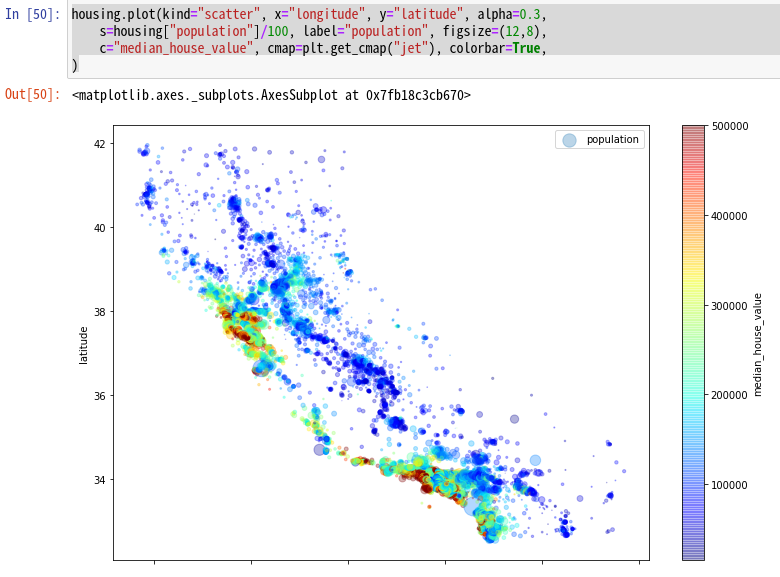
housing.plot(kind="scatter", x="longitude", y="latitude", alpha=0.3,
s=housing["population"]/100, label="population", figsize=(12,8),
c="median_house_value", cmap=plt.get_cmap("jet"), colorbar=True,
)
こちらが実行結果だ。赤いところが家の価格も高いことがわかる。また内陸ほど、人口も少く家の価格も安いこともこの散布図から簡単にわかる。つまり、San FranciscoとL.A.周辺は家の価格が高いことが、この地図からわかる。
相関について: corr()メソッド
Pearsonの相関係数 r は、2つの変数の間にある線形な関係性を図る指標だ。1~-1の間の数値になり、1の場合右肩あがりのグラフになり、-1だと右肩下がりのグラフになる。
0の場合は、無相関である。
pandasのcorr()メソッドを使って、各列の間の相関係数が計算され、結果はpandas.DataFrameで返る。
これをprintで表示しても、このように正直理解しずらい。
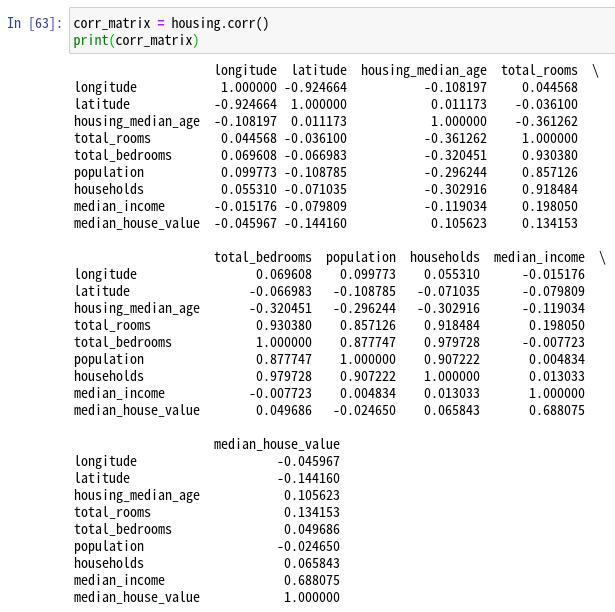
そこで、media_incomeとの相関係数のみソートして表示してみよう。するとこのように、昇順でわかりやすくなる。

median_incomeが、0.688ともっとも相関関係にあることがわかる。
まあ、当たり前と言えばそれまでだが、どれぐらい相関関係にあるのかをデータが証明してくれる。
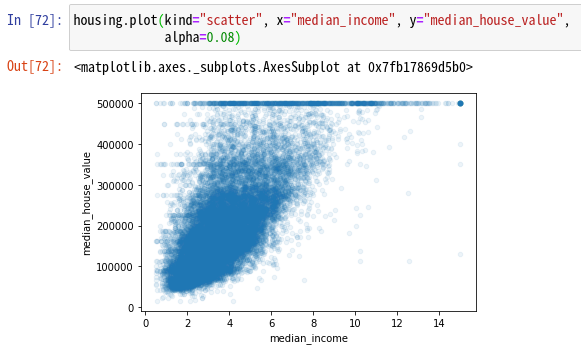
このmedian_house_valueとmedian_incomeの散布図を描くと右肩上がりの関係性と$50,000や$45,000や$35,000あたりにmedian_house_valueが集中していることがわかる。
まとめ
pandasのplot()メソッドを使うことによって、経度と緯度情報から簡単に散布図が作成できた。別の見方をすると、この散布図は地図情報とも言える。
cmapで色情報を追加すると、より視覚的に家の値段を表現することができる。
最後に、相関係数を表示することで、どれほど相関関係にあるのか数値で比較することが容易にできることがわかった。
https://matplotlib.org/tutorials/introductory/pyplot.html
https://matplotlib.org/tutorials/colors/colormaps.html
Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow, 2nd Edition by Aurélien Géron Published by O’Reilly Media, Inc., 2019, Ch2



コメント